|
The problem #23 of 2015 US Physics Olympiad F=ma Exam generated a bit of controversy as people had slight difficulty dealing with spring that was already compressed at the initial state. The controversy was compounded by some typos in the released solution. The version here might be easier for some people to understand. Please check it and suggest any way to improve it. After deriving all the equation parts in the solution, we can gain physical insight into the situation. We may argue that the mechanical energy of the system can be separated into portion related to the smaller mass that was dropped, and larger mass that already was in sort of equilibrium with the spring, thus be effectively set to zero. It can be viewed that dropping of the smaller mass is what introduced the new mechanical energy into the system, thus we only need to worry about how the smaller mass oscillates within the system as any part of mechanical energy related to the movement of the larger mass will always balance out to zero. Then the oscillating movement of the smaller mass, of which the larger mass will duplicate due to being stuck to the smaller mass, is dependent only on the kinetic energy it introduce to the system ( KE ), gravitational potential energy of the smaller mass( m1 gx), and the additional contraction/extension of the spring induced by the impact of the smaller mass ( ½ k x^2 ), while the gravitational potential energy of the larger mass can be ignored due to existing compression of the spring before the impact.
0 Comments
|
Archives
April 2022
AuthorComplete Learning Academy Categories |
Our Services
|
Resources |
Complete Learning Academy |
Copyright ©2021 | 135 Cumberland Rd. Suite #201, Pittsburgh, PA | 412-701-1011 | [email protected]
Some images are designed by Freepick


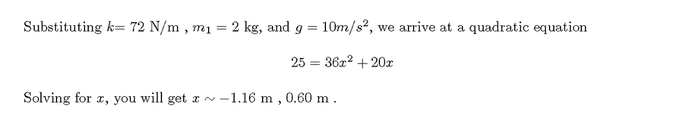
 RSS Feed
RSS Feed
